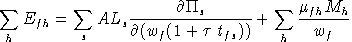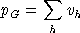An Algebraic Statement of the Samuelson Model
Zero Net Profit for Private Production
The unit cost of production in sector As is given
by a nested Leontief - Cobb-Douglas function defined over the cost of
intermediate inputs and primary factors with ad-valorem taxes on
factor demands. Unlike the Harberger models, tax rates in this model
are determined endogenously. In equilibrium, the unit cost must be
no less than the market price of output:
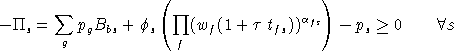
Zero Net Profit for Public Sector Contractors
The unit cost of public provision is determined by the market price
of commodity inputs to the Leontief activity. Input requirements are
defined by a vector of public sector input coefficients,
ag. In equilibrium, the price paid by the
government equals the cost of market inputs:
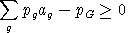
Income Balance for Government
Government tax income (PT) is determined by the value of tax
revenue, calculated using activity levels, compensated demands,
market prices and ad-valorem tax rates. In equilibrium, the value of
tax revenue equals the market cost of public sector output:
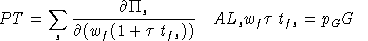
Income Balance for Households
Household income is determined by the net of tax return to primary factors
plus the imputed value of public provision:
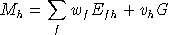
Market Clearance for Private Goods
Producer output is equal to the sum of intermediate plus final demand:
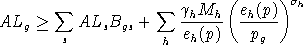 where
where
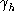 is the household budget share devoted to the
consumption of goods, and eh is the "unit expenditure
function" which may be written:
is the household budget share devoted to the
consumption of goods, and eh is the "unit expenditure
function" which may be written:
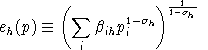
Personalized Markets for Public Goods
We assume a "pure" public good in this model, hence each household
may attach a different marginal valuation to public provision in an
equilibrium. In order to compute these marginal values, we include a
separate public good "market" for each houshold which balances the
level of provision with the household "demand":
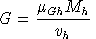 .
.
in which
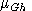 is the budget share of public goods in
the top-level Cobb-Douglas preferences of household h.
is the budget share of public goods in
the top-level Cobb-Douglas preferences of household h.
Market Clearance for Factors
The aggregate supply of factors equals the sum of producer and
consumer demand. Producers pay taxes on factor inputs, consumers do
not because we consider these demands to be "leisure" or "household
production". Consumer demands for factors are specified as
Cobb-Douglas (constant budget shares):
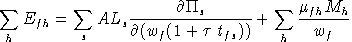
Samuelson Rule for "Optimal" Provision of Public Goods
The tax rate multiplier is adjusted to balance the marginal cost of
public provision with the summation across households of marginal
willingness to pay. Due to the existence of household factor demand,
factor taxes are necessarily distortionary and there will be an
excess social cost of public funds. For this reason, the Samuelson
rule is neither necessary nor sufficient for optimal provision. We
apply the rule here merely to illustrate the programming methodology,
even though the resulting equilibrium may be "suboptimal":
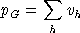
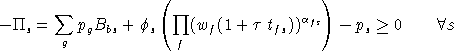
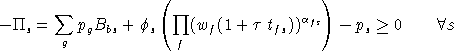
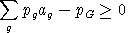
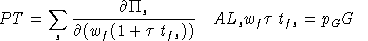
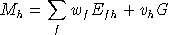
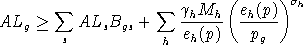
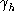 is the household budget share devoted to the
consumption of goods, and eh is the "unit expenditure
function" which may be written:
is the household budget share devoted to the
consumption of goods, and eh is the "unit expenditure
function" which may be written: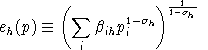
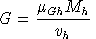 .
.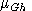 is the budget share of public goods in
the top-level Cobb-Douglas preferences of household h.
is the budget share of public goods in
the top-level Cobb-Douglas preferences of household h.