

GAMS is a high level modeling system for mathematical programming and optimization. It consists of a language compiler and a range of associated solvers.
The GAMS modeling language allows modelers to quickly translate real world optimization problems into computer code. The gams language compiler then translates this code into a format the solvers can understand and solve. This architecture provides great flexibility, by allowing changing the solvers used without changing the model formulation.
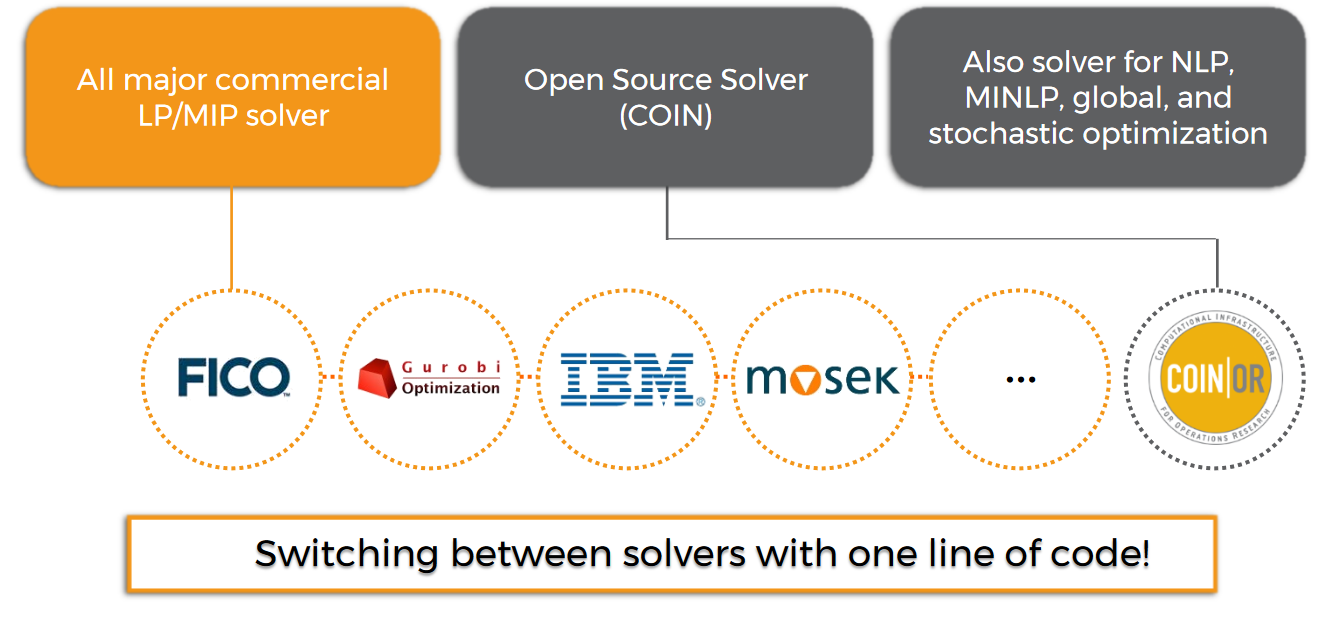
GAMS Free Solvers and Links included in the GAMS Base distribution
Additional solvers can be purchased through us.
The GAMS language provides a natural way to describe your model. This is best highlighted with a commonly used simple example by Dantzig (1963):
The goal is minimization of the cost of shipping goods from two plants to three markets, subject to supply and demand constraints.
Indices
$i = $plants
$j = $markets
Given data
$a_{i} = $supply of commodity of plant $i$ (cases)
$b_{j} = $demand for commodity at market $j$ (cases)
$d_{ij} = $distance between plant $i$ and market $j$ (thousand miles)
$c_{ij} = F \times d_{ij}$ shipping cost per unit shipment between plant $i$ and market $j$ (dollars per case per thousand miles)
| Plants ↓ | New-York | Chicago | Topeka | ← Markets |
|---|---|---|---|---|
| Seattle | 2.5 | 1.7 | 1.8 | 350 |
| San-Diego | 2.5 | 1.8 | 1.4 | 600 |
| Demand → | 325 | 300 | 275 | ↑ supply |
$F=$ $ per thousand miles
Decision variables
$x_{ij} = $amount of commodity to ship from plant $i$ to market $j$ (cases), where $x_{ij} \ge 0$, for all $i,j$
Constraints
Observe supply limit at plant $i: \sum_{j}{x_{ij}} \le a_{i}$ for all $i$ (cases)
Satisfy demand at market $j: \sum_{i}{x_{ij}} \ge b_{j}$ for all $j$ (cases)
Objective Function
Minimize $\sum_{i}\sum_{j}c_{ij}x_{ij}$ ($K)
The above can easiliy be formulated using the GAMS language. The use of concise algebraic descriptions makes the model highly compact, with a logical structure. Internal documentation, such as explanation of parameters and units of measurement, makes the model easy to read.
Sets
i canning plants / Seattle, San-Diego /
j markets / New-York, Chicago, Topeka / ;
Parameters
a(i) capacity of plant i in cases
/ Seattle 350
San-Diego 600 /
b(j) demand at market j in cases
/ New-York 325
Chicago 300
Topeka 275 / ;
Table d(i,j) distance in thousands of miles
New-York Chicago Topeka
Seattle 2.5 1.7 1.8
San-Diego 2.5 1.8 1.4 ;
Scalar f freight in dollars per case per thousand miles /90/ ;
Parameter
c(i,j) transport cost in thousands of dollars per case ;
c(i,j) = f * d(i,j) / 1000 ;
Variables
x(i,j) shipment quantities in cases
z total transportation costs in thousands of dollars ;
Positive variables x ;
Equations
cost define objective function
supply(i) observe supply limit at plant i
demand(j) satisfy demand at market j ;
cost .. z =e= sum((i,j), c(i,j)*x(i,j)) ;
supply(i) .. sum(j, x(i,j)) =l= a(i) ;
demand(j) .. sum(i, x(i,j)) =g= b(j) ;
Model transport /all/ ;
Solve transport using LP minimizing z ;
This short code-listing demonstrates the most important syntax features of the GAMS language. Below we will go through the individual statements one by one:
Sets are the basic building blocks of a GAMS model, corresponding exactly to the indices in the algebraic representations of models. The Transportation example above contains just one Set statement:
Sets
i canning plants / Seattle, San-Diego /
j markets / New-York, Chicago, Topeka / ;
The effect of this statement is probably self-evident. We declared two sets and gave them the names $i$ and $j$. We also assigned members to the sets as follows:
$i =$ {Seattle, San-Diego}
$j =$ {New-York, Chicago, Topeka}.
Note the use of forward slashes ("/") for surrounding the list of set members. In mathematical notation this would be done with curly braces instead.
Parameters are one way of entering data in GAMS. In this case, the parameters $a$ and $b$ are defined over the sets $i$ and $j$.
Parameters
a(i) capacity of plant i in cases
/ Seattle 350
San-Diego 600 /
b(j) demand at market j in cases
/ New-York 325
Chicago 300
Topeka 275 / ;
GAMS lets you place explanatory text (shown in lower case) throughout your model, as you develop it. Your comments are automatically incorporated into the output report, at the appropriate places.
Data can also be entered in convenient table form. GAMS lets you input data in their basic form - transformations are specified algebraically.
Table d(i,j) distance in thousands of miles
New-York Chicago Topeka
Seattle 2.5 1.7 1.8
San-Diego 2.5 1.8 1.4 ;
Constants can simply be declared as scalars:
Scalar f freight in dollars per case per thousand miles /90/ ;
When data values are to be calculated, you first declare the parameter (i.e. give it a symbol and, optionally, index it), then give its algebraic formulation. GAMS will automatically make the calculations.
Parameter
c(i,j) transport cost in thousands of dollars per case ;
c(i,j) = f * d(i,j) / 1000 ;
Decision variables are expressed algebraically, with their indices specified. From this general form, GAMS generates each instance of the variable in the domain. Variables are specified as to type: FREE, POSITIVE, NEGATIVE, BINARY, or INTEGER. The default is FREE. The objective variable (z, here) is simply declared without an index.
Variables
x(i,j) shipment quantities in cases
z total transportation costs in thousands of dollars ;
Positive variables x ;
Objective function and constraint equations are first declared by giving them names. Then their general algebraic formulae are described. GAMS now has enough information (from data entered above and from the algebraic relationships specified in the equations) to automatically generate each individual constraint statement - as you can see in the output report below. An extensive set of tools enables you to model any expression that can be stated algebraically: arithmetic, indexing, functions and exception-handling log (e.g. if-then-else and such-that constructs).
=E= indicates ’equal to’
=L= indicates ’less than or equal to’
=G= indicates ‘greater than or equal to’
Equations
cost define objective function
supply(i) observe supply limit at plant i
demand(j) satisfy demand at market j ;
cost .. z =e= sum((i,j), c(i,j)*x(i,j)) ;
supply(i) .. sum(j, x(i,j)) =l= a(i) ;
demand(j) .. sum(i, x(i,j)) =g= b(j) ;
The model is given a unique name (here, TRANSPORT), and the modeler specifies which equations should be included in this particular formulation. In this case we specified ALL which indicates that all equations are part of the model. This would be equivalent to MODEL TRANSPORT /COST, SUPPLY, DEMAND/ . This equation selection enables you to formulate different models within a single GAMS input file, based on the same or different given data.
Model transport /all/ ;
The solve statement (1) tells GAMS which model to solve, (2) selects the solver to use (in this case an LP solver), (3) indicates the direction of the optimization, either MINIMIZING or MAXIMIZING , and (4) specifies the objective variable.
Solve transport using LP minimizing z ;