

This paper describes a new programming environment for economic equilibrium analysis. The system embeds the Mathematical Programming System for General Equilibrium analysis (MPSGE, Rutherford (1987)) within the Generalized Algebraic Modeling System (GAMS, Brooke, Kendrick and Meeraus (1988)). This arrangement exploits GAMS' set-oriented algebraic syntax for data manipulation and report writing. The new system uses an extension of the MPSGE input format to provide a compact, non-algebraic representation of a model's nonlinear equations. This paper provides an overview of the modeling environment and three worked examples in tax policy analysis.
MPSGE is a modeling language specially designed for solving Arrow-Debreu economic equilibrium models. (See Rutherford (1987, 1989).) The name stands for "mathematical programming system for general equilibrium". The idea of the MPSGE program is to provide a transparent and relatively painless way to write down and analyze complicated systems of nonlinear inequalities. The language is based on nested constant elasticity of substitution utility functions and production functions. The data requirements for a model include share and elasticity parameters for all the consumers and production sectors included in the model. These may or may not be calibrated from a consistent benchmark equilibrium dataset.
GAMS, the "Generalized Algebraic Modeling System", is a modeling language which was originally developed for linear, nonlinear and integer programming. This language was developed over 15 years ago by Alex Meeraus when he was working at the World Bank. (See Brooke, Kendrick and Meeraus (1988).) Since that time, GAMS has been widely applied for large-scale economic and operations research modeling projects.
MPSGE and GAMS embody different philosophies in their designs. MPSGE is appropriate for a specific class of nonlinear equations, while GAMS is capable of representing any system of algebraic equations. While GAMS is applicable in several disciplines, MPSGE is only applicable in the analysis of economic models within a particular domain. The expert knowledge embodied in MPSGE is of particular use to economists who are interested in the insights provided by formal models but who are unable to devote many hours to programming. MPSGE provides a structured framework for novice modellers. When used by experts, MPSGE reduces the setup cost of producing an operational model and the cost of testing alternative specifications.
Prior to the connection with GAMS, the "achilles heel" of MPSGE had been the process by which input data was translated into the tabular format of the MPSGE input file. For small models, this translation was not difficult. Given a calibrated "benchmark equilibrium dataset", a couple of hours with a word processor is usually enough time to generate and investigate a moderately large model. If, however, a model involves several classes of sectors and agents, a wide range of tax instruments and large tables of input data, the word- processor approach is impossible. When there are many numbers, there are many opportunities for oversights and typographical errors.
In contrast, the GAMS modeling language is designed for managing large datasets. The use of sets and detached-coefficient matrix notation makes the GAMS environment very nice for both developing balanced benchmark datasets and for writing solution reports. For large complicated models, a shortcoming of the GAMS modeling environment lies in the specification of the nonlinear equations. Economic equilibrium models, particularly those based on complicated functions such as nested CES, are easier to understand at an abstract level than they are to specify in detail, and the translation of a model from input data into algebraic relations can be a tedious and error- prone undertaking.
The interface between GAMS and MPSGE combines the strengths of both programs. The system uses GAMS as the "front end" and "back end" to MPSGE facilitating data handling and report writing. The language employs an extended MPSGE syntax based on GAMS sets, so that model specification is very concise. In addition, the system includes two large-scale solvers, MILES (Rutherford (1993)) and PATH (Ferris and Dirkse (1993)), which may be used interchangeably. The availability of two algorithms greatly enhances robustness and reliability.
The remainder of this paper is organized as follows. Section 2 introduces MPSGE input syntax and the GAMS interface using a small two-sector model of taxation. Section 3 extends the 2x2 model to illustrate how the software is used to perform equal-yield (differential) tax policy analysis and to analyze tax reform in a model with endogenous taxation. Section 4 provides a brief summary and conclusion. The paper introduces language features largely through example. Details on language syntax and program structure are provided in two appendices. Appendix A provides a complete statement of MPSGE syntax and a summary of differences with the original (1989) language. Appendix B provides an overview of the modeling environment and the structure of GAMS input files which employ MPSGE.
Before proceeding, both to placate impatient readers and to provide some hands-on experience for novices, I recommend that readers install the GAMS system, then retrieve and process the library file THREEMGE which contains three MPSGE models (HARBERGER, SHOVEN and SAMUELSON). Two commands to retrieve and run these models:
gamslib threemge
gams threemge
After having processed this file, print the listing files
(THREEMGE.LST) for reference.
2 THE MATHEMATICAL FORMULATION
Mathiesen (1985) demonstrated that an Arrow-Debreu general economic
equilibrium model could be formulated and efficiently solved as a
complementarity problem. Mathiesen's formulation may be posed in
terms of three sets of "central variables":
p = a non-negative n-vector of commodity prices including all final goods, intermediate goods and primary factors of production;
y = a non-negative m-vector of activity levels for constant returns to scale production sectors in the economy; and
M = an h-vector of income levels, one for each "household" in the model, including any government entities.
An equilibrium in these variables satisfies a system of three classes of nonlinear inequalities.
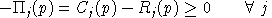
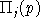 is the unit profit function, the difference
between unit revenue and unit cost, defined as:
is the unit profit function, the difference
between unit revenue and unit cost, defined as: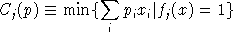
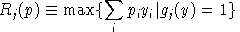
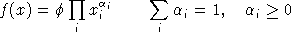
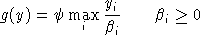
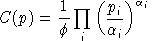
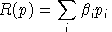
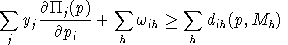
Final demand are derived from budget-constrained utility maximization:
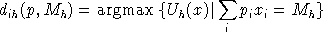
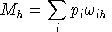
We always work with utility functions which exhibit non-satiation, so
Walras' law will always hold:
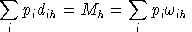 .
.
Aggregating market clearance conditions using equilibrium prices and
the zero profit conditions using equilibrium activity levels, it then
follows that:
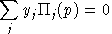
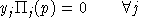 .
.
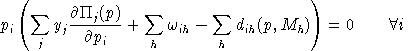 .
.In other words, complementary slackness is a feature of the equilibrium allocation even though it is not imposed as an equilibrium condition, per-se. This means that in equilibrium, an production activity which is operated makes zero profit and any production activity which earns a negative net return is idle. Likewise, any commodity which commands a positive price has a balance between aggregate supply and demand, and any commodity in excess supply has an equilibrium price of zero.
3 A SMALL EXAMPLE
This section of the paper introduces MPSGE model
building using a two- good, two-factor (2x2) example. This is
addressed to readers who may be unfamiliar with GAMS
and/or the original (scalar) MPSGE syntax. The
discussion provides some details on the formulation and specification
of one small model from the MPSGE library.
Subsequently, two extensions are presented, one which illustrates
equal yield constraints and another which introduces a pure public
good. These examples are by no means exhaustive of the classes of
equilibrium structures which can be investigated using the software,
but they do provide a starting point for new users.
The structure of MPSGE model HARBERGER is "generic" Arrow-Debreu with taxes. Households obtain income by supplying factors of production to industry or collecting tax revenue. This income is then allocated between alternative goods in order to maximize welfare subject to the budget constraint.
Firms operate subject to constant returns to scale, selecting factor inputs in order to minimize cost subject to technological constraints. For an algebraic description of a model closely related to this one, see Shoven and Whalley (1984). The present model differs in two respects from the Shoven-Whalley example. First, in this model there are intermediate inputs to production while in the Shoven-Whalley model goods are produced using only value-added. Second, this model incorporates a labor-leisure choice so that the excess burden of factor taxes here incorporates the disincentive to work associated with a lower net wage.
Sectors Consumers ------------------------------------ X Y OWNERS WORKERS GOVT ------------------------------------ PX 100 -20 -30 -50 PY -10 80 -40 -30 PK -20 -40 60 PL -50 -10 100-40 ------------------------------------ TRNS 10 20 -30 TK -20 -10 30 ------------------------------------
The input data is presented in the form of a balanced matrix, the entries in which represent the value of economic transactions in a given period (typically one year). Social accounting matrices (SAMs) can be quite detailed in their representation of an economy, and they are also quite flexible. All sorts of inter-account taxes, subsidies and transfers can be represented through an appropriate definition of the accounts.
Traditionally, a SAM is square with an exact correspondence between rows and columns. (For an introduction, see Pyatt and Round, "Social Accounting Matrices: A Basis for Planning", The World Bank, 1985.) The numbers which appear in a conventional SAM are typically positive, apart from very special circumstances, whereas the rectangular SAM displayed in Table 1 follows a sign convention wherein supplies or receipts are represented by positive numbers and demands or payments are represented by negative numbers. Internal consistency of a rectangular SAM implies that row sums and column sums are zero. This means that supply equals demand for all goods and factors, tax payments equal tax receipts, there are no excess profits in production, the value of each household expenditure equals the value of factor income plus transfers, and the value of government tax revenue equals the value of transfers to households.
With simple MPSGE models, it is convenient to use a rectangular SAM format. This format emphasizes how the MPSGE program structure is connected to the benchmark data. In the rectangular SAM, we have one row for every market (traded commodity). In the present model, there are four markets, for goods X and Y and factors L and K.
There are two types of columns in the rectangular SAM, corresponding to production sectors and consumers. In the present model, there are two production sectors (X and Y) and three consumers (OWNERS, WORKERS and GOVT).
Now that we have identified the underlying sets, we may interpret the input matrix as a set of parameters with which we can easily specify the benchmark equilibrium. (See Table 2.) It is quite common to begin a general equilibrium modeling project with a large input-output table or social accounting matrix which may then be mapped onto a number of submatrices, each of which is dimensioned according to the underlying sets used in the model.
Sectors Consumers
------------------------------------------
(S) Households(H) Government
------------------------------------------
Goods Markets (G): A(G,S)-B(G,S) -C(G,H)
Factor Markets (F): -FD(F,S) E(F,H)-D(F,H)
Capital taxes: -T("K",S) GREV
Transfers: TRN(H) -GREV
The GAMS specification of benchmark data is presented in Table 3 which begins with a statement of the underlying sets (G, F, H). The statement "ALIAS (S,G);" simply says that S and G both reference {X,Y}. Thereafter follows the social accounting data table and declarations for the various submatrices. The parameters ELAS() and ESUB() are elasticities ("free parameters") which can be chosen independently from the benchmark accounts. The parameters TF and PF are calibrated tax and reference price arrays which are computed given benchmark factor and tax payments. (In this model, average and marginal tax rates are not distinguished, so the benchmark marginal tax rate is simply the tax payment divided by the net factor income.)
A general equilibrium model determines only relative prices. For purposes of reporting or constructing value-indices, we use Laspeyres quantity index, THETA(G), the elements of which correspond to shares of aggregate consumer expenditure in the benchmark period.
* SECTION (i) DATA SPECIFICATION AND BENCHMARKING
SETS G GOODS AND SECTORS /X, Y/,
F PRIMARY FACTORS /K, L/,
H HOUSEHOLDS /OWNER, WORKER/;
ALIAS (S,G);
TABLE SAM(*,*) SOCIAL ACCOUNTING MATRIX
X Y OWNER WORKER GOVT
X 100 -20 -30 -50
Y -10 80 -40 -30
K -20 -40 60
L -50 -10 60
TK -20 -10 30
TRN 10 20 -30
PARAMETER
A(S) BENCHMARK OUTPUT
B(G,S) USE MATRIX (GOODS INPUTS BY SECTOR)
C(G,H) HOUSEHOLD DEMAND
FD(F,S) FACTOR DEMAND BY SECTOR
E(F,H) FACTOR ENDOWMENTS
D(F,H) FACTOR DEMAND BY HOUSEHOLDS
T(F,S) TAX PAYMENT BY FACTOR BY SECTOR
TRN(H) TRANSFER REVENUE
ELAS(S) ELASTICITY OF SUBSTITUTION IN PRODUCTION
ESUB(H) ELASTICITY OF SUBSTITUTION IN DEMAND
GREV BENCHMARK GOVERNMENT REVENUE
TF(F,S) FACTOR TAX RATE
PF(F,S) BENCHMARK FACTOR PRICES GROSS OF TAX
THETA(G) WEIGHTS IN NUMERAIRE PRICE INDEX
WBAR(H) BENCHMARK WELFARE INDEX;
* EXTRACT DATA FROM THE SOCIAL ACCOUNTING MATRIX:
A(S) = SAM(S,S);
B(G,S) = MAX(0, -SAM(G,S));
C(G,H) = -SAM(G,H);
FD(F,S) = -SAM(F,S);
E(F,H) = SAM(F,H);
D(F,H) = 0;
TRN(H) = SAM("TRN",H);
T("K",S) = -SAM("TK",S);
* INSTALL "FREE" ELASTICITY PARAMETERS:
E("L","WORKER") = 100;
D("L","WORKER") = 40;
ELAS(S) = 1;
ESUB(H) = 0.5;
* INSTALL FUNCTIONS OF BENCHMARK VALUES:
GREV = SUM(H, TRN(H));
TF(F,S) = T(F,S) / FD(F,S);
PF(F,S) = 1 + TF(F,S);
THETA(G) = SUM(H, C(G,H));
THETA(G) = THETA(G) / SUM(S, THETA(S));
WBAR(H) = SUM(G, C(G,H)) + SUM(F, D(F,H));
One $PROD: block describes the single class of production activities, and two $DEMAND: blocks characterize endowments and preferences for the two classes of consumers.
Consider the records associated with production sector AL(S). The entries on the first line of a $PROD: block are elasticity values. The "s:0" field indicates that the top-level elasticity of substitution between inputs is zero (Leontief). The entry "a:ELAS(S)" indicates that inputs identified as belonging to the "a:" aggregate trade off with an elasticity of substitution ELAS(S) (at the second level of the production function). In these production functions, the primary factors (W(F)) are identified as entering in the a: aggregate.
* SECTION (ii) MPSGE MODEL DECLARATION
$ONTEXT
$MODEL:HARBERGER
$SECTORS:
AL(S)
$COMMODITIES:
P(G) W(F) PT
$CONSUMERS:
RA(H) GOVT
$PROD:AL(S) s:0 a:ELAS(S)
O:P(S) Q:A(S)
I:P(G) Q:B(G,S)
I:W(F) Q:FD(F,S) P:PF(F,S) A:GOVT T:TF(F,S) a:
$DEMAND:RA(H) s:1 a:ESUB(H)
D:P(G) Q:C(G,H) a:
D:W(F) Q:D(F,H)
E:W(F) Q:E(F,H)
E:PT Q:TRN(H)
$DEMAND:GOVT
D:PT Q:GREV
$REPORT:
V:CD(G,H) D:P(G) DEMAND:RA(H)
V:DF(F,H) D:W(F) DEMAND:RA(H)
V:EMPLOY(S) I:W("L") PROD:AL(S)
V:WLF(H) W:RA(H)
$OFFTEXT
* Invoke the preprocessor to declare the model for GAMS:
$SYSINCLUDE mpsgeset HARBERGER
* ------------------------------------------------------------------
* SECTION (iii) BENCHMARK REPLICATION
HARBERGER.ITERLIM = 0;
$INCLUDE HARBERGER.GEN
SOLVE HARBERGER USING MCP;
ABORT$(ABS(HARBERGER.OBJVAL) GT 1.E-4)
"*** HARBERGER benchmark does not calibrate.";
HARBERGER.ITERLIM = 1000;
The records within a $PROD: block begin with "O:" or "I:". An "O:" indicates an output and an "I:" represents an input. In both types of records, "Q:" is a "quantity field" indicating a reference input or output level of the named commodity. A "P:" signifies a reference price field. This price is measured as a user cost, gross of applicable taxes. The default values for reference price and reference quantity are both unity (i.e., a value of 1 is installed if a P: or Q: field is missing).
The A: and T: fields in a $PROD: block indicate tax agent and ad-valorem tax rate, respectively. The tax agent is specified before the tax rate. A single input or output coefficient may have two or more taxes applied. Consumers are treated symmetrically, and there is thus no restriction on the consumer to whom the tax is paid. Typically, however, one consumer is associated with the government.
To better understand the relationship between reference prices and tax rate specification, consider inputs of W.K to sector AL.X in this model. The benchmark payment to capital in the X sector is 20 and the tax payment is 20. Hence the ad-valorem tax rate in the benchmark equilibrium is 100% ( T:1), and the reference price of capital, market price of unity times (1 + 100%), is 2 (P:2). If in a counterfactual experiment the tax rate on capital inputs to sector X is altered, this will change the T: field but it will not change the P: field. Q: and P: characterize a reference equilibrium point, and these are therefore unaffected by subsequent changes in the exogenous parameters.
It is important to remember that the $PROD:AL(S) block represents as many individual production functions as there are elements in set S (two in this case). Within the $PROD:AL(S) block, inputs refer to sets G and F , while the output coefficient, O:P(S), refers only to set S. Sets referenced within a commodity name in an I: or O: field may be sets which are "controlled" by the sets referenced in the function itself, in which case only a scalar entry is produced. In $PROD:AL(S) there are only outputs of commodity S in sector S.
The first line of a $DEMAND block also contains fields (e.g., s:, a:, b: etc.) which represent elasticities of substitution. The subsequent records may begin with either an E: field or a D: field. These, respectively, represent commodity endowments and demands. In the demand fields, the P: and Q: entries are interpreted as reference price and reference quantity, analogous to the input fields in a $PROD block. Ad-valorem taxes may not be applied on final demands, so that if consumption taxes are to be applied in a model they must be levied on production activities upstream of the final demand.
The benchmark values for all activity levels and prices are equal to the default value of unity, and therefore we are able to specify values in the Q: fields directly from the benchmark data. An equivalent model could be specified in which the benchmark activity levels for AL(S) equal, for example, A(S,S). This would then require rescaling the input and output coefficients for those sectors, and it would not necessarily be helpful, because in a scaled model it is more difficult to verify consistency of the benchmark accounts and MPSGE input file. Furthermore, for numerical reasons it is advisable to scale equilibrium values for the central variables to be close to unity.
Government transfers to households are accomplished through the use of an "artificial commodity" (PT). The government is identified as the agent who receives all tax revenue (see the A:GOVT entry in both of the $PROD: blocks). Commodity PT is the only commodity on which GOVT spends this income, hence government tax revenue is divided between the two households in proportion to their endowments of the artificial good. In order to scale units so that the benchmark price of PT is unity, the $30 of government tax revenue chases 10 units of PT assigned to OWNER and 20 units assigned to WORKER. (See values for TRN(H) in Table 3.)
The $REPORT section of the input file requests the solution system to return values for inputs, outputs, final demands or welfare indices at the equilibrium. Only those items which are requested will be written to the solution file. Each record in the report block begins with a V: (variable name) field. These names must be distinct from all other names in the model. The second field of the report record must have one of the labels I:, O: or D: followed by a commodity name, or the label W: followed by a consumer name. The third field's label must be "PROD:" in an I: or O: record, and it must be "DEMAND:" if it is a D: record.
An algebraic formulation of the Harberger model is provided for the interested reader.
(i) The elasticities together with the reference quantities and reference prices of inputs and outputs completely characterize the underlying nested CES functions. No other data fields in the $PROD: block alters the technology. If, for example, a tax rate changes as part of a counter-factual experiment, this has no effect on the reference price. The value in the P: field depends on the benchmark value of the T: field if the model has been calibrated, but subsequent changes in T: do not change the underlying technology.
(ii) Tax rates are interpreted differently for inputs and outputs. The tax rate on inputs is specified on a net basis, while the tax rate on outputs is specified on a gross basis. That is, the user cost of an input with market price p subject to an ad-valorem tax at rate t is p (1 + t), while the user cost of an output subject to an ad-valorem tax at rate t is p (1 - t). (A tax increases the producer cost of inputs and decreases the producer value of outputs.)
MPSGE provides a limited number of economic components with which complex models can be constructed. There are some models which lie outside the MPSGE domain, but in many cases it is possible to recast the equilibrium structure in order to produce an MPSGE model which is logically equivalent to the original model - usually after having introduced some sort of artificial commodity or consumer. In the present model, the use of commodity PT to allocate government revenue between households provides a fairly typical example of how this can be done. In the process of making such a transformation, one often gains a meaningful economic insight.
The output file (not shown) also provides details on the computational process. For an explanation of these statistics, see Rutherford (1993).
---- VAR AL
LOWER LEVEL UPPER MARGINAL
X . 1.000 +INF .
Y . 1.000 +INF .
---- VAR P
LOWER LEVEL UPPER MARGINAL
X . 1.000 +INF .
Y . 1.000 +INF .
---- VAR W
LOWER LEVEL UPPER MARGINAL
K . 1.000 +INF .
L . 1.000 +INF .
LOWER LEVEL UPPER MARGINAL
---- VAR PT . 1.000 +INF .
---- VAR RA
LOWER LEVEL UPPER MARGINAL
OWNER . 70.000 +INF .
WORKER . 120.000 +INF .
LOWER LEVEL UPPER MARGINAL
---- VAR GOVT . 30.000 +INF .
---- VAR CD
LOWER LEVEL UPPER MARGINAL
X.OWNER . 30.000 +INF .
X.WORKER . 50.000 +INF .
Y.OWNER . 40.000 +INF .
Y.WORKER . 30.000 +INF .
---- VAR DF
LOWER LEVEL UPPER MARGINAL
K.OWNER . . +INF EPS
K.WORKER . . +INF EPS
L.OWNER . . +INF EPS
L.WORKER . 40.000 +INF .
---- VAR EMPLOY
LOWER LEVEL UPPER MARGINAL
X . 50.000 +INF .
Y . 10.000 +INF .
---- VAR WLF
LOWER LEVEL UPPER MARGINAL
OWNER . 1.000 +INF .
WORKER . 1.000 +INF .
**** REPORT SUMMARY : 0 NONOPT
0 INFEASIBLE
0 UNBOUNDED
0 ERRORS
* ------------------------------------------------------------------
* SECTION (iv) COUNTER-FACTUAL SPECIFICATION AND SOLUTION:
SET SC COUNTERFACTUAL SCENARIOS TO BE COMPUTED /
L UNIFORM TAX ON LABOR,
K UNIFORM TAX ON CAPITAL,
VA UNIFORM VALUE-ADDED TAX/
PARAMETER TAXRATE(F,S,SC) COUNTERFACTUAL TAX RATES,
REPORT(*,*,*,SC) SOLUTION REPORT - % CHANGES,
PINDEX PRICE DEFLATOR;
* SPECIFY COUNTER-FACTUAL TAX RATES TO ACHIEVE CETERIS
* PARIBUS BALANCED BUDGET:
TAXRATE("L",S,"L") = GREV / SUM(G, FD("L",G));
TAXRATE("K",S,"K") = GREV / SUM(G, FD("K",G));
TAXRATE("L",S,"VA") = GREV / SUM((F,G), FD(F,G));
TAXRATE("K",S,"VA") = GREV / SUM((F,G), FD(F,G));
LOOP(SC,
* INSTALL TAX RATES FOR THIS COUNTERFACTUAL:
TF(F,S) = TAXRATE(F,S,SC);
$INCLUDE HARBERGER.GEN
SOLVE HARBERGER USING MCP;
* ------------------------------------------------------------------
* SECTION (v) REPORT WRITING:
* REPORT SOME RESULTS:
PINDEX = SUM(G, P.L(G) * THETA(G));
REPORT("REVENUE","_",SC) = 100 * (PT.L/PINDEX - 1);
REPORT("TAXRATE","_",SC) =
100 * SMAX((F,S), TAXRATE(F,S,SC));
REPORT("WELFARE",H,SC) = 100 * (WLF.L(H) - 1);
REPORT("EMPLOY",S,SC) = 100 * (EMPLOY.L(S)/FD("L",S) - 1);
REPORT("PRICE",G,SC) = 100 * (P.L(G)/PINDEX - 1);
REPORT("PRICE",F,SC) = 100 * (W.L(F)/PINDEX - 1);
REPORT("OUTPUT",S,SC) = 100 * (AL.L(S) - 1);
);
DISPLAY REPORT;
4 ALTERNATIVE MODELS
The "standard" MPSGE model is based on fixed
endowments and tax rates, but many empirical models do not fit into
this structure. For example, in the model HARBERGER, the
level of each replacement tax was specified to be consistent with
"equal yield", but as a result of the endogenous response of prices
and quantities, the resulting tax revenues differed significantly
from the benchmark levels. For example, when the capital tax is
replaced by a uniform labor tax at a rate which, in the absence of
labor supply response, produces "equal yield", we find that tax
revenue in fact declines by 39%. In order to perform differential
(equal yield) tax policy analysis, it is therefore necessary to
accommodate the endogenous determination of tax rates as part of the
equilibrium computation. This is one of many possible uses of
"auxiliary variables" in MPSGE.
Within MPSGE, auxiliary variables can either represent price-adjustment instruments (endogenous taxes) or they can represent a quantity-adjustment instruments (endowment rations). In model SHOVEN, TAU is used to proportionally scale factor taxes in order to achieve a target level of government revenue. The auxiliary variable first appears in the $PROD:AL(S) block, following the declaration of a tax agent. There are two fields associated with an endogenous tax. The first field (N:) gives the name of the auxiliary variable which will scale the tax rate. The second field (M:) specifies the multiplier. If the M: field is omitted, the multiplier assumes a default value of unity. If the value in the M: field is zero, the tax does not apply.
The auxiliary variable TAU also appears at the bottom of the file where it labels an associated inequality constraint. This constraint exhibits complementary slackness with the associated non-negative auxiliary variable (i.e., if TAU is positive, the constraint must hold with an equality, whereas if the constraint is non-binding TAU must be zero). An auxiliary variable may or may not appear in its associated constraint.
The constraint associated with TAU is based on a price index defined by THETA(G). The constraint assures a level of tax revenue such that the value of transfers to households is held constant. (Endowments of the commodity PT are fixed, so when the value of PT is fixed, then so too are the value of transfers from GOVT to each of the households.)
SHOVEN illustrates how an auxiliary variable can be interpreted as a tax instrument. In the MPSGE syntax, auxiliary variables may also be employed to endogenously determine commodity endowments. There is no restrictions on how a particular auxiliary variable is to be interpreted. A single variable could conceivably serve simultaneously as an endogenous tax as well as a endowment ratio, although this would be rather unusual.
MPSGE PREPROCESSOR VERSION 1/94 286/386/486 DOS
0 $MODEL: SHOVEN
1
2 $SECTORS:
3 AL(S)
4
5 $COMMODITIES:
6 P(G) W(F) PT
7
8 $CONSUMERS:
9 RA(H) GOVT
10
11 $AUXILIARY:
12 TAU
13
14 $REPORT:
15 V:CD(G,H) D:P(G) DEMAND:RA(H)
16 V:DF(F,H) D:W(F) DEMAND:RA(H)
17 V:EMPLOY(S) I:W("L") PROD:AL(S)
18 V:WLF(H) W:RA(H)
19
20 $PROD:AL(S) s:0 a:ELAS(S)
21 O:P(G) Q:A(G,S)
22 I:P(G) Q:B(G,S)
23 I:W(F) Q:FD(F,S) P:PF(F,S)
24 + A:GOVT N:TAU$TF(F,S) M:TF(F,S)$TF(F,S) a:
25
26 $DEMAND:RA(H) s:1 a:ESUB(H)
27 D:P(G) Q:C(G,H) a:
28 D:W(F) Q:D(F,H)
29 E:W(F) Q:E(F,H)
30 E:PT Q:TRN(H)
31
32 $DEMAND:GOVT
33 D:PT Q:GREV
34
35 $CONSTRAINT:TAU
36 PT =G= SUM(G, THETA(G) * P(G));
37
38 $OFFTEXT
An algebraic formulation of the Shoven model is provided for the interested reader.
The relevant characteristic of a pure public good entering final demand is that each consumer "owns" the same quantity. Agents' attitudes toward public goods differ, and because there is no market, agents' valuations of the public good will also differ. In an MPSGE model, the separate valuations are accommodated through the introduction of "personalized" markets for public good - one market for each consumer. In the model, consumer expenditure encompasses both private and public "purchases", and consumer income encompasses both private and public "endowments". An individual is endowed with a quantity of her own version of the public good determined by the level of public expenditures. An increase in taxes, to the extent that it increases tax revenue, will increase the level of public provision.
In this model, the structure of relative factor taxes is exogenous but the aggregate level of taxes is not. Tax rates are scaled up or down so that the sum of individual valuations of the public good (the marginal benefit) equals the cost of supply of the public good (the direct marginal cost).
Consider features of model SAMUELSON which do not appear in SHOVEN:
(i) There are new commodities PG and VG(H). The first of these represents the direct marginal cost of public output from sector GP, a Leontief technology which converts private goods inputs into the public good. For the SAMUELSON structure, all government revenues apply to purchases of the public good (observe that the only good demanded by consumer GOVT is PG ). The prices VG(H) represent the individual consumer valuations of the public good. Commodity VG(H) appears only in the endowments and demands of consumer RA(H). The endowment record for VG(H) includes a quantity V(H) which is the benchmark valuation of the public good by agent H.
(ii) There are two auxiliary variables. TAU has the same interpretation as in the SHOVEN, determining the aggregate tax level. Auxiliary variable LGP is a rationing instrument representing an index of the "level of public goods provision", scale to equal 1 in the benchmark. Consumer RA(H) thus is endowed with a quantity of VG(H) given by V(H) * LGP .
(iii) The constraint for TAU in SAMUELSON differs from the TAU constraint in SHOVEN. Here the constraint represents the Samuelson condition, equating the marginal cost (PG*GREV) and the sum of individuals' marginal benefit ( SUM(H,VG(H)*V(H)) ). The constraint for LGP simply assigns LGP equal to the sector GP activity level. (The LGP variable and constraint are only needed because the R: field only accepts auxiliary variables.)
MPSGE PREPROCESSOR VERSION 1/94 286/386/486 DOS
0 $MODEL: SAMUELSON
1
2 $SECTORS:
3 AL(S) GP
4
5 $COMMODITIES:
6 P(G) W(F) PG VG(H)
7
8 $CONSUMERS:
9 RA(H) GOVT
10
11 $AUXILIARY:
12 TAU LGP
13
14 $REPORT:
15 V:CD(G,H) D:P(G) DEMAND:RA(H)
16 V:DF(F,H) D:W(F) DEMAND:RA(H)
17 V:EMPLOY(S) I:W("L") PROD:AL(S)
18 V:WLF(H) W:RA(H)
19
20 $PROD:AL(S) s:0 a:ELAS(S)
21 O:P(G) Q:A(G,S)
22 I:P(G) Q:B(G,S)
23 I:W(F) Q:FD(F,S) P:PF(F,S)
24 + A:GOVT N:TAU$TF(F,S) M:TF(F,S)$TF(F,S) a:
25
26 $PROD:GP s:0
27 O:PG Q:GREV
28 I:P(G) Q:GD(G)
29
30 $DEMAND:RA(H) s:1 a:ESUB(H)
31 D:P(G) Q:C(G,H) a:
32 D:W(F) Q:D(F,H)
33 D:VG(H) Q:V(H)
34 E:VG(H) Q:V(H) R:LGP
35 E:W(F) Q:E(F,H)
36
37 $DEMAND:GOVT
38 D:PG Q:GREV
39
40 $CONSTRAINT:TAU
41 GREV * PG =G= SUM(H, V(H) * VG(H));
42
43 $CONSTRAINT:LGP
44 LGP =G= GP;
45
46 $OFFTEXT
An algebraic formulation of the Samuelson model is provided for the interested reader.
INDEX 1 = HARBERGER
K L VA
REVENUE._ 3.9 -38.9 -0.8
TAXRATE._ 50.0 50.0 25.0
WELFARE.OWNER 1.9 42.4 18.5
WELFARE.WORKER -0.1 -26.8 -10.9
WELFARE.TOTAL 0.6 -1.3 -3.48143E-2
EMPLOY .X -5.3 -6.9 -8.4
EMPLOY .Y 20.5 34.4 22.1
PRICE .X -10.4 -11.2 -10.3
PRICE .Y 11.8 12.8 11.8
PRICE .K 3.9 59.5 24.5
PRICE .L -4.7 -38.9 -23.5
OUTPUT .X 3.6 -1.0 0.4
OUTPUT .Y -3.7 2.0 -2.0
INDEX 1 = SHOVEN
K L VA
TAXRATE._ 47.1 134.2 25.3
WELFARE.OWNER 3.3 40.2 18.3
WELFARE.WORKER -1.0 -29.2 -10.8
WELFARE.TOTAL 0.6 -3.6 -3.51710E-2
EMPLOY .X -5.0 -19.7 -8.5
EMPLOY .Y 21.5 12.1 21.9
PRICE .X -10.4 -9.0 -10.3
PRICE .Y 11.9 10.2 11.8
PRICE .K 6.2 49.8 24.2
PRICE .L -5.0 -56.5 -23.6
OUTPUT .X 3.6 -7.9 0.3
OUTPUT .Y -3.4 -2.0 -2.1
INDEX 1 = SAMUELSON
K L VA
REVENUE ._ -1.4 -14.5 -6.7
TAXRATE ._ 45.7 88.8 22.8
WELFARE .OWNER 4.7 43.9 21.1
WELFARE .WORKER -2.0 -31.4 -12.9
WELFARE .TOTAL 0.5 -3.7 -0.4
EMPLOY .X -4.9 -7.5 -5.9
EMPLOY .Y 24.5 37.5 29.7
PRICE .X -10.7 -11.3 -10.9
PRICE .Y 12.2 13.0 12.5
PRICE .K 7.8 60.3 29.0
PRICE .L -6.0 -51.8 -24.5
OUTPUT .X 3.0 -2.2 0.9
OUTPUT .Y -2.3 3.3 -2.58148E-2
PROVISION._ -0.8 -13.9 -6.1
5 SUMMARY
This paper has provided an introduction to a new GAMS
subsystem for applied general modeling. This extension of GAMS
accomodates a tabular representation of highly nonlinear cost and
expenditure functions through which model specification is concise
and transparent. The paper has presented three small examples which
illustrate the programming environment and its application to
traditional economic issues in public finance for which applied
general equilibrium analysis is a standard tool.
Further work is underway in the development and evaluation of solution algorithms for applied general equilibrium models implemented within GAMS/MPSGE. In addition to providing a convenient framework for model- builders, the new GAMS/MPSGE system also simplifies the implementation and testing of algorithms for complementarity problems. Information on the relative effectiveness of different solution strategies should prove quite helpful to users who are using the system to solve very large systems of nonlinear equations.
Brooke, T., D. Kendrick and A. Meeraus (1988) GAMS: A User's Guide, The Scientific Press, Redwood City, California.
Rutherford, T. (1993) "MILES: A Mixed Inequality and nonLinear Equation Solver", Working Paper, Department of Economics, University of Colorado.
Rutherford, T. (1987) "Applied General Equilibrium Modeling", Ph.D. thesis, Department of Operations Research, Stanford University.
Rutherford, T.F. (1989) "General Equilibrium Modeling with MPSGE", The University of Western Ontario.
Shoven, J. and J. Whalley (1984) "Applied General Equilibrium Models of Taxation and International Trade: Introduction and Survey", Journal of Economic Literature 22, 1007-1051.
Thompson, G. and S. Thore (1992) Computational Economics , Scientific Press, Redwood City, California.
- End-of-line is significant. Continuation lines are indicated by a "+" in column 1.
- In general, input is not case sensitive, except in the specification of sub-nests for production and demand functions.
- Numeric expression involving GAMS parameters or constants must be enclosed in parentheses.
$ONTEXT
Indicate the beginning of a GAMS comment block containing an MPSGE model.
$MODEL:model_name
model_name must be a legitimate file name. This name is subsequently used to form MODEL_NAME.GEN (this file name must be upper case when running under UNIX).
$SECTORS:, $COMMODITIES:, $AUXILIARY:, $CONSUMERS:Four keywords define variables which are used in the model. Entries in these blocks share the same syntax. The $AUXILIARY block is only used in models with side constraints and endogenous taxes or rationed endowments.
$PROD:sectorProduction functions must be specified for each production sector in the model.
$DEMAND:consumer
Demand functions must be specified for every consumer in the model. General structure is the same as for production functions above.
$CONSTRAINT:auxiliary
Specifies a side constraint to be associated with a specified auxiliary variable.
$REPORT:
Identifies the set of additional variables to be calculated. These include outputs and inputs by sector and demands by individual consumers.
$OFFTEXTIndicates the end of model specification.
The $SECTORS:, $COMMODITIES:, $CONSUMERS: and $AUXILIARY: blocks contain implicit GAMS variable declarations in which the index sets must be specified in the GAMS program above and the variable names must be distinct from all other symbols in the GAMS program. One or more variables may be declared per line separated by one or more spaces.
$SECTORS:
Y(R,T) ! Output in region R in period T
K(T) ! "Aggregate capital stock, period T"
In these declarations, the trailing comments (signified by "!") are interpreted as variable name descriptors which subsequently appear in the solution listing.
The equivalent GAMS declaration for these variables would be:
VARIABLES Y(R,T) Output in region R in period T
K(T) "Aggregate capital stock, period T";
As with the usual GAMS syntax, when a variable descriptor contains a punctuation symbol such as ",", it is required to enclosed in quotes.
$SECTORS:
X(R,T)$(X0(R) GT 0)
Here, the GAMS conditional operator "$" is used to restrict the domain of the variable X. The expression following the dollar sign is passed through to the GAMS compiler and must conform to GAMS syntax rules.
$SECTORS:
X Y(R)$Y0(R) Z ! Descriptor for Z
W(G,R,T) ! Descriptor for W
More than one symbol may appear on a single line. The descriptor only applies to the last one.
All MPSGE variables must be declared. When multidimensional variables are specified, they must be declared explicitly - declarations like X(*) are not permitted. Two further restrictions are that the sets used in the declaration must be static rather than dynamic, and any variable which is declared must be used in the model. There is a simple way to work around these restrictions. Let me illustrate with an example. Suppose that in a model the set of production sectors AL is employed for all elements of a static set S which satisfy a particular condition, for example BMX(S) not equal to 0. This would require that AL be declared as follows:
$SECTORS: AL(S)$BMX(S)
In this context, the symbol "$" is used as an "exception operator" which should be read as "such that". In this case, we have generated one AL sector for each element of the set S for which BMX(S) is nonzero.
$PROD:Y(R) s:1
O:P(R) Q:Y0(R)
I:W(F,R) Q:FD0(F,R)
This block characterizes a Cobb-Douglas production function in which the elasticity of substitution between inputs is one - "s:1" in the first line which sets a top level substitution elasticity equal to unity. Variable Y(R) is an activity level declared within the $SECTORS: block. Variables P(R) and W(F,R) are prices declared within the $COMMODITIES: block. The O: label indicates an output, and the I: prefix indicates an input. The Q: fields in both records represent "reference quantities". Y0(R) and FD0(F,R) must be GAMS parameters defined previously in the program.
$PROD:X(R) s:ESUB(R) a:0 b:(ESUB(R)*0.2)
O:PX Q:X0(R)
I:PY(G) Q:YX0(G,R) a:
I:PL Q:LX0(R) b:
I:PK Q:KX0(R) b:
The keyword line specifies three separate elasticities related to this function. ESUB(R) is the top level elasticity of substitution. There are two sub-nests in the function. Nest a: is a Leontief nest (in which the compensated elasticity is zero). The elasticity of subtitution in nest b: is one-fifth of the top level elasticity.
In the function specification, commodities PY(G) (one input for each element of set G) enter in fixed proportions. Commodities PL and PK enter in nest b.
If this function has been specified using a balance benchmark dataset with reference prices equal to unity, then the following identity should be satisfied:
X0(R) = SUM(G, YX0(G,R)) + LX0(R) + KX0(R)
$PROD:AL(S) s:0 a:ELAS(S)
O:P(G) Q:A(G,S)
I:P(G) Q:B(G,S)
I:W(F) Q:FD(F,S) P:PF(F,S) A:GOVT T:TF(F,S) a:
In this function, we have two new ideas. The first is the use of a reference price denoted by "P:". This entry indicates that the function should be calibrate to a reference point where individual input prices (gross of tax) equal PF(F,S). If P: does not appear, prices of one are assumed.
The second new idea here is that taxes may be levied on production inputs. The A: label identifies the name of the tax agent (a $CONSUMER:). The T: label identifies the ad-valorem tax rate.
$DEMAND:RA(R)$RA0(R) s:1
E:PL Q:LE(R)
D:P(G)$DG(G) Q:D0(G,R)$DD(G,R) P:P0(G,R)
This function specification demonstrates the use of conditionals. This function is only generated when RA0(R) is nonzero. The demands D: for a particular element of set G are suppressed entirely when DG(G) equals 0. The Q: field also has an exception operator, so that the default value for Q: (unity) is applied when DD(G,R) equals zero.
This example is somewhat artificial, but it illustrates the distinction between how exception operators affect lead entries (I:, O:, D: and E:) and subsequent entries. When an exception is encountered on the lead entry, the entire record may be suppressed. Exceptions on subsequent entries only applied to a single field.
The valid labels in a function declaration ($PROD: or $DEMAND:) line include:
| s: | Top level elasticity of substitution between inputs or demands. |
| t: | Elasticity of transformation between outputs in production. (valid only in $PROD blocks) |
| a:,b:,... | Elasticities of substitution in individual input nests. |
The recognized labels in an I: or O: line include:
| Q: | Reference quantity. Default value is 1. When specified, it must be the second entry. |
| P: | Reference price. Default value is 1. |
| A: | Tax revenue agent. Must be followed by a consumer name. |
| T: | Tax rate field identifier. (More than one tax may apply to a single entry.) |
| N: | Endogenous tax. This label must be followed by the name of an auxiliary variable. |
| M: | Endogenous tax multiplier. The advalorem tax rate is the product of the value of the endogenous tax and this multiplier. |
| a:,b:,.. | Nesting assignments. Only one such label may appear per line. |
The valid labels in an E: line include:
| Q: | Reference quantity |
| R: | Rationing instrument indicating an auxiliary variable. |
The valid labels in a D: line include:
| Q: | Reference quantity |
| P: | Reference price |
| a:,b:... | Nesting assignment |
Complementarity conditions apply to upper and lower bounds on auxiliary variables and the associated constraints. For this reason, the orientation of the equation is important. When an auxiliary variable is designated POSITIVE (the default), the auxiliary constraint should be expressed as a "greater or equal" inequality (=G=). If an auxiliary variable is designated FREE, the associated constraint must be expressed as an equality (=E=).
$CONSTRAINT:TAU
G =G= X * Y;
$CONSTRAINT:MU(I)$MU0(I)
MU(I) * P(I) * Q(I) =G= SUM(J, THETA(I,J) * PX(J));
The exception applied in this example restricts the equation only to those elements of set I for which MU0(I) is not zero.
The general form is as follows:
$REPORT:
V:variable name I:commodity PROD:sector
V:variable name O:commodity PROD:sector
V:variable name D:commodity DEMAND:consumer
V:variable name W:consumer
The first row returns an input quantity, the second row returns an output quantity, the third returns a demand quantity, and the fourth row returns a consumer welfare index. (Note: the level value returned for a "consumer variable" is an income level, not a welfare index.)
$REPORT:
V:DL(S) I:PF("L") PROD:Y(S)
V:DK(S) I:PF("K") PROD:Y(S)
V:SX(G,S)$SX0(G,S) O:PX(G) PROD:X(S)
V:D(G,H) D:P(G) DEMAND:RA(H)
V:W(H) W:RA(H)
Note that the "$" exception is only meaninful on the first entry. Also notice that the domain of the report variable must conform to the domain of the subsequent two entries.
(iii) Case folding: In the vector syntax, upper and lower case letters are not distinguished. The entire file is processed as though it were written in upper case. This is not compatible with the earlier version of MPSGE in which "P" and "p" were distinct.
(iii) Distinct names: Names used for variables in the MPSGE model must be distinct from each other as well as from all other symbols in the GAMS program. If there is a GAMS set or parameter or model named X, then X may not be used to identify an MPSGE sector or commodity.
(iv) Tabs: MPSGE fields are free format and tabs are translated to spaces by the preprocessor. Tabs are permitted in GAMS provided that the compiler is properly configured (under DOS, "TABIN 8" must be inserted in file GAMSPARM.TXT in the GAMS system directory).
$PROD:X(S)$T(S)
... ! sector X described for S in T
$PROD:X(S)$(NOT T(S))
... ! sector X described for S not in T.
The preprocessor does not require one and exactly one declaration for each sector. If multiple declarations appear, the later set of coefficients overwrites the earlier set.
$ECHOP: logical Default=.FALSE.
is a switch for returning all or part of the scalar MPSGE file to the solver status file. In order to have this output printed in the listing file, enter the GAMS statement "OPTION SYSOUT=ON;" prior to solving the model.
$PEPS: real Default=1.0E-6
is the smallest price for which price-responsive demand and supply functions are evaluated. If a price is below PEPS, it is perturbed (set equal to PEPS) prior to the evaluation.
$EULCHK: logical Default=.TRUE.
is a switch for evaluating Euler's identity for homogeneous equations. The output is useful for monitoring the numerical precision of a Jacobian evaluation. When a price or income level is perturbed in a function, the Euler check may fail.
$WALCHK: logical Default=.TRUE.
is a switch for checking Walras's law. Like EULCHK, this switch is provided primarily to monitor numerical precision. When an income level is perturbed, the Walras check may fail.
$FUNLOG: logical Default=.FALSE.
is a switch to generate a detailed listing of function evaluations for all production sectors and consumers.
FUNLOG triggers a function evaluation report which provides detailed output describing the evaluation of supply and demand coefficients. The information provide is sufficient that an industrious graduate student should be able to reproduce the results (given a pencil, paper and slide rule).
The evaluation report has the following headings:
| T | Coefficient "type" with the following interpretation: | |
| IA | Input aggregate | |
| OA | Output aggregate | |
| I | Input | |
| O | Output | |
| D | Demand | |
| E | Endowment | |
| N | Name (either nest identifier or commodity name) | PBAR | Benchmark price (the P: field value) |
| P | Current price (gross of tax) | |
| QBAR | Benchmark quantitity (the Q: field value) | |
| Q | Current quantity | |
| KP | Identifier for parent entry in nesting structure. | |
| ELAS | Associated elasticity (input or output aggregates only) |
When $FUNLOG:.TRUE is specified, a complete report of demand and supply coefficients for every production and demand function in every iteration. Be warned that with large models this can produce an enrmous amount of output!
The following two function evaluation reports are generated in the first iteration in solving case "L" for model HARBERGER:
Function Evaluation for: AL.X T N PBAR P QBAR Q KP ELAS ------------------------------------------------------------------------ IA s 1.0000E+00 8.9198E-01 1.0000E+02 1.0000E+02 0.00 OA t 1.0000E+00 1.0000E+00 1.0000E+02 1.0000E+02 0.00 IA a 1.0000E+00 8.7998E-01 9.0000E+01 9.0000E+01 s 1.00 O P.X 1.0000E+00 1.0000E+00 1.0000E+02 1.0000E+02 t I P.Y 1.0000E+00 1.0000E+00 1.0000E+01 1.0000E+01 s I W.K 2.0000E+00 1.5000E+00 2.0000E+01 2.3466E+01 a I W.L 1.0000E+00 1.0000E+00 5.0000E+01 4.3999E+01 a Function evaluation for: RA.OWNER T N PBAR P QBAR Q KP ELAS ------------------------------------------------------------------------ IA s 1.0000E+00 1.0000E+00 7.0000E+01 7.0000E+01 1.00 OA t 1.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.00 IA a 1.0000E+00 1.0000E+00 7.0000E+01 7.0000E+01 s 0.50 D P.X 1.0000E+00 1.0000E+00 3.0000E+01 3.0000E+01 a D P.Y 1.0000E+00 1.0000E+00 4.0000E+01 4.0000E+01 a E W.K 1.0000E+00 1.0000E+00 6.0000E+01 0.0000E+00 E PT 1.0000E+00 1.0000E+00 1.0000E+01 0.0000E+00
$DATECH: logical Default=.FALSE.
is a switch to generate a annotated listing of the function and Jacobian evaluation including a complete listing of all the nonzero coefficients.
MPSGE generates an analytic full first-order Taylor series expansion of the nonlinear equations in every iteration. Nonzero elements of the Jacobian matrix are passed to the system solver (MILES or PATH) which uses this information in the direction-finding step of the Newton algorithm. Coefficients are produced with codes which help interpret where they came from. The following codes are used:
Needless to say, the $DATECH:.TRUE. switch produces a very big status file for large models. It is not something which is very useful for the casual user.
Here is a partial listing of nonzeros generated during the first linearization for scenario "L" in model HARBERGER:
---------------------------------------- Coefficients for sector:AL.X P.X AL.X 1.0000E+02 B AL.X P.X -1.0000E+02 B P.Y AL.X -1.0000E+01 B AL.X P.Y 1.0000E+01 B W.K AL.X -2.3466E+01 B AL.X W.K 3.5199E+01 B W.L AL.X -4.3999E+01 B AL.X W.L 4.3999E+01 B W.K W.K 1.3037E+01 E0 1.3037E+01 W.K W.L -1.3037E+01 E0 -1.3037E+01 W.L W.K -1.9555E+01 E0 -1.9555E+01 W.L W.L 1.9555E+01 E0 1.9555E+01 GOVT AL.X -1.1733E+01 B GOVT W.K -1.1733E+01 E1 GOVT W.K 6.5184E+00 E0 6.5184E+00 GOVT W.L -6.5184E+00 E0 -6.5184E+00 ---------------------------------------- Income for consumer:RA.OWNER W.K 6.0000E+01 W0 RA.OWNER W.K -6.0000E+01 B PT 1.0000E+01 W0 RA.OWNER PT -1.0000E+01 B RA.OWNER RA.OWNER 1.0000E+00 B ---------------------------------------- Demands for consumer:RA.OWNER P.X -3.0000E+01 W0 P.Y -4.0000E+01 W0 P.X P.X 8.5714E+00 E0 8.5714E+00 P.X P.X 1.2857E+01 E0 1.2857E+01 P.X P.Y -8.5714E+00 E0 -8.5714E+00 P.X P.Y 1.7143E+01 E0 1.7143E+01 P.Y P.X -8.5714E+00 E0 -8.5714E+00 P.Y P.X 1.7143E+01 E0 1.7143E+01 P.Y P.Y 8.5714E+00 E0 8.5714E+00 P.Y P.Y 2.2857E+01 E0 2.2857E+01 P.X RA.OWNER -4.2857E-01 E0 -3.0000E+01 P.Y RA.OWNER -5.7143E-01 E0 -4.0000E+01
APPENDIX B: FILE STRUCTURE
This appendix provides an overview of the structure of
GAMS input files which include MPSGE
models. The text of the paper presents many of these ideas by way of
example, but it may also be helpful for some users to have a
"template" for constructing MPSGE models. The
discussion in this section focuses on a "generic" input file, the
schematic form of which is presented in Table 10. This section first
presents a "top down" view of program organization, and then it
discusses aspects of the new syntax for model specification.
Users who are unfamiliar with GAMS can consult the manual. Beginning GAMS programmers should remember that the MPSGE interface to GAMS is unlike other solution subsystems. "Level values" are passed between the GAMS program and MPSGE in the usual fashion, but MPSGE models do not require the explicit use of the VARIABLE or EQUATION statements.)
The second section of the file consists of a GAMS comment range, beginning with an $ONTEXT record and ending with an $OFFTEXT record, followed by an invocation of the preprocessor. The preprocessor writes operates on statements in the MPSGE model declaration which are "invisible" to the GAMS compiler. This program reads the MPSGE model statements and generates GAMS-readable code, including a model_name.gen file. Additional GAMS code produced by the preprocessor includes declarations for each of the central variables and report variables in the MPSGE model.
The third section of the generic input file performs a "benchmark replication" and may not be present in all applications. There are four statements required for benchmark validation. The first statement sets the iteration limit to be zero; the second statement causes the MPSGE model to be "generated", and the third statement causes the MPSGE solver to read the model and return the deviations. In this call, the level values passed to the solver are unaltered because the iteration limit is zero. Market excess supplies and zero profit checks are returned in the "marginals" of the associated commodity prices and activity levels, respectively. The final statement in this section resets the iteration limit to 1000 (the default value) for subsequent counter-factual computations.
Section (iv) defines and then computes a counter-factual equilibrium. A counter-factual equilibrium is defined by parameter values such as tax rates or endowments which take on values different from those in the benchmark equilibrium. Within the GAMS interface to MPSGE, it is also possible to fix one or more central variables. When any variable is fixed, the associated equation is omitted from the equilibrium system during the solution process but the resulting imbalance is then reported in the solution returned through the marginal.
The final section of the file represents the GAMS algebra required for comparing counter-factual equilibria. It would be possible, for example, to construct welfare measures or to report percentage changes in certain values. All of these calculations are quite easy because the equilibrium values are returned as level values in the associated variables.
For large models, the advantage of the vector format is that by using appropriately defined GAMS sets, the number of individual functions which need to be defined is reduced only to the number of "classes" of functions. This makes it possible to represent large dimensional models using only a few lines of code.
To summarize, here are the basic features of a program which uses GAMS as a front-end to MPSGE:
(i) An MPSGE model is defined within a GAMS comment range followed by
$sysinclude mpsgeset model_name
(ii) Every SOLVE statement for a particular model is preceded by $INCLUDE MODEL.GEN. The GEN file is written by the preprocessor based on the model structure.
(iii) Solution values for the cental variables in the MPSGE model and any declared "report variables" are returned in GAMS variable level values. Level values for slacks are returned as "marginals" for the associated variables.
(iv) The model description follows a format which is a direct extension of the scalar data format. Certain aspects of the new language, such as case folding, are incompatible with the original MPSGE syntax.